本人初中生,思维水平比较活跃,喜欢折腾一些新奇玩意,可能表达上有些不对的地方
我刚开始写的时候没想那么多,但是逐渐的我发现我的表达能力有所欠缺,我意识到我的问题:
我的思维的成长速度大于了表达速度
所以这篇文章是我删删改改一周才完成的作品,希望大家认真品读
引言
在平面直角坐标系中,我们通常将横轴、纵轴分别表示自变量和因变量.但在实际应用中,坐标轴可以代表任意物理量,比如电压、电流、功率等.
坐标系变换这个想法其实对于我源于一道物理题,
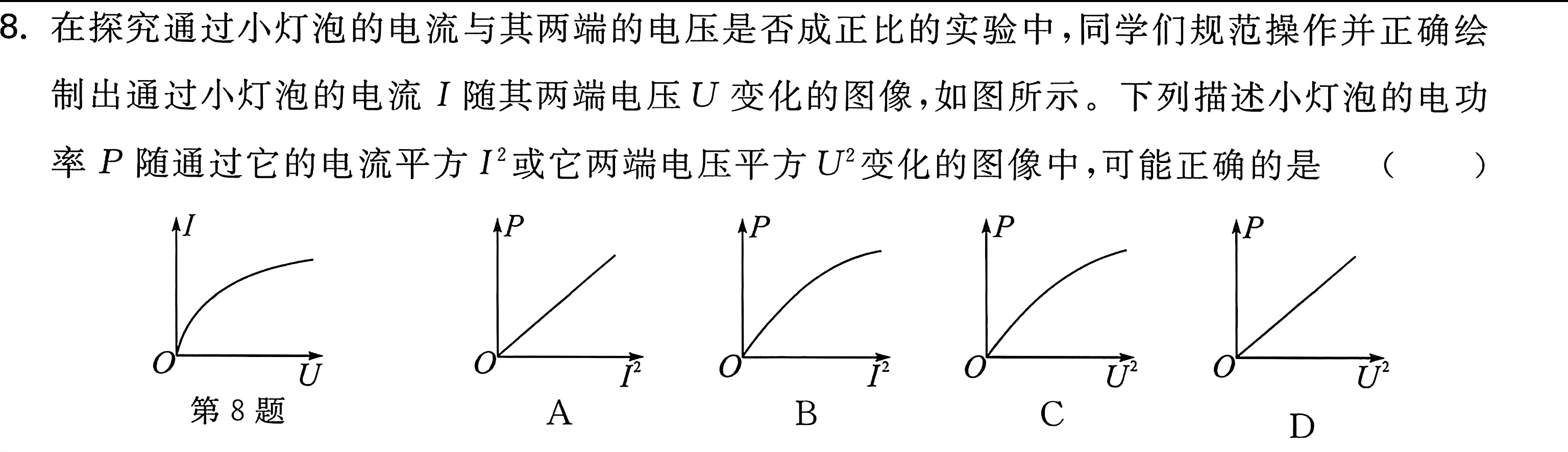
这道题其实可以直接分析电阻来判断图像
但是我想到了不同的思路
对于横坐标 $P$ ,我们可以展开为 $U$ 与 $I$ 的乘积,然后对于A选项和B选择这种类型,横坐标是 $I^2$ ,纵坐标是 $UI$ ,于是我萌生一种想法,是不是坐标轴的 $I$ 可以互相约掉,如果可以,那么约掉 $I$ 的坐标轴就是 $U$ 与 $I$ ,正好与原图像横纵坐标相反,于是得到这个图像与第八题给的图矛盾,正好横纵坐标颠倒了,所以错误了.
这种分析方式对于 B,C 类型的坐标系也适用,展开后"化简"得到的横轴是 $U$ ,纵轴是 $I$ ,C选项正好符合原图,所以答案是C
这个似乎看着很合理的想法被我进行了扩展,如果对坐标轴进行非线性变换,函数图像会发生怎样的变化?
这个想法让我对坐标轴变换进行了一系列探索,带给了我很多惊喜,那么让我们开始吧
理论前提
为了让大部分人听懂,我会先进行一些基础讲解,这些是必要的
点与坐标系的关系
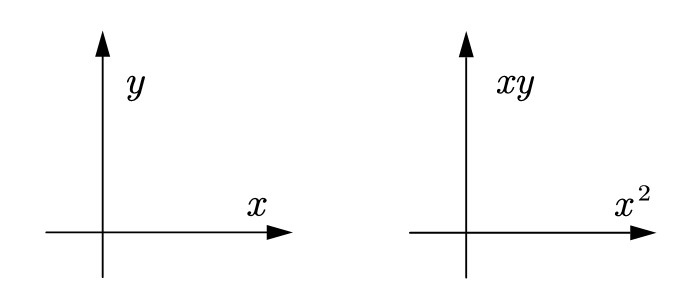
看这两个坐标系,有什么不同?
显而易见,第一个是普通的坐标系,而第二个坐标轴发生变化
如果给你一个点 $(x,y)$ ,在不同坐标系下它的意义是不同的
点本身没有意义,意义是坐标轴赋予的
在几何坐标系中,$(x,y)$ 表示位置;
在物理坐标系中,$(x,y)$ 代表系统状态;
而在经过非线性变换的坐标系中,它所描述的是某种复合量或能量等级
所以,改变坐标轴,并不是改变世界,而是改变我们看世界的方式.
那么我改变了坐标轴,它的意义到底变成啥了?
对于普通的坐标系, $x,y$ 的意义就是向右的距离和向上的距离,这就是它本身的用途
而像第二个图,它的意义发生了改变,具体是什么改变我们要引入函数
引入函数
为什么要引入函数呢?
很简单,因为如果没有函数,这个图几乎就毫无意义
为什么我说几乎没有意义,因为不一定是函数,只是函数可以描述规则,你可以这么理解
一个点在坐标系中有没有意义,取决于你给这个坐标系赋予了什么规则,而函数只是其中一种规则
对于这种非线性的坐标系,坐标轴不再是“横竖距离”,而是两个参数在一个非线性空间中的位置编号
如果你仅仅定义坐标轴表示什么,而不规定一些规则,那么这个图毫无意义,没人能解释它
而物理量,函数则是为坐标系提供了一个规则
是不是有点抽象?我拿函数举例你就明白了
当我引入函数 $f(x)$ ,第一个坐标系的 $x$ 可以代表自变量的取值,而 $y$ 就代表 $f(x)$ 的值
同样的,第二个坐标系的 $x^2$ 可以代表自变量的平方,而 $xy$ 则是自变量和函数值的积
值得注意的是,因为你已经规定 $x$ 是 $f(x)$ 的自变量了,所以在第二个坐标系中你要避免使用 $(x,y)$ 这种变量形式表述坐标,因为在命名上有冲突
可以用 $(a,b)$ 或者 $(x^2,xy)$ 表示一个点,这一步曾困扰过我
如果你看得没有这么透彻,可以用换元思想,令 $X=x^2,Y=xy$ ,这样可以描述一个点的坐标为 $(X,Y)$ ,你甚至可以让一个函数的自变量为 $X$ ,这样就可以写做 $f(X)$ 或 $f(x^2)$ ,这样这个函数在图像上就和 $f(x)$ 在普通坐标系的图像相同了.一个很好的理解方式就是你换元后 $X$ 即是坐标轴,又是函数 $f(X)$ 的自变量,仅仅只是换了个表述形式,他们实际意义不变.就像在不同角度看世界
从位置编号与实际意义角度出发
我们讲非线性坐标系的坐标轴是两个参数在一个非线性空间中的位置编号
这个在普通坐标系也适用,因为对于每一个点也不过是一个位置编号罢了
对于普通坐标系, $f(x)$ 上一点 $(a,b)$ 是一个位置编号.在引入函数的先提下,它可以代表 $f(x)$ 的自变量为 $a$ 时 $f(x)$ 的值为 $b$
对于第二个坐标系, $(a,b)$ 也是位置编号,不过它的意义是当 $x^2=a$ 时, $f\left( x \right) \cdot x$ 的值为 $b$
探索
假设一种非线性坐标轴变换(和原来一样):
我们把两个坐标轴都乘$x$,那么x轴所代表的意义是 $x^2$ ,y轴所代表的意义是$xy$
我们把它抽象为平面坐标$(x, y)$,函数表示为:
$$y = f(x)$$
假设函数在原坐标系上有一点$(x, y)$
现在对坐标系做如下非线性变换:
$$X = x^2, \quad Y = x y$$
横坐标 $X$ = 原横坐标的平方
纵坐标 $Y$ = 原横坐标乘以纵坐标
我们讨论过位置编号与实际意义的关系
这里显然 $(X,Y)$ 是位置编号
我们设想如果变换前后位置编号不发生改变,函数应该满足怎样的关系
$$(x, y) \longrightarrow (X, Y) = (x^2, x f(x))$$
位置编号不发生改变,所以
$$x=X,y=Y$$
$$x=x^2,f\left( x \right) =f\left( x \right) \cdot x$$
这个条件太苛刻了,我们尝试保持变换前后每个点意义不变,然后看看怎么用新的函数表示出来
如果一个点 $(x,y)$ 变换后意义不变,那么
$$Y = x \cdot f(x), \quad X = x^2$$
只要用 X 表示 Y,就能知道在新坐标系 Y与X的关系,进而我们可以得出它与 $f(X)$ 图像上的差异
可以得到
$$x=\sqrt{X}, \quad Y=\sqrt{X}f\left( \sqrt{x} \right) $$
所以原本的一条函数曲线,在新的坐标系中被“扭曲”了,这就是非线性变换的本质影响
函数成正比例
我们需要对一些案例进行分析,这也是我整个思考的过程
比如正比例函数,即 $y=kx$ ,
因为$X=x^2,Y=xy$
很容易想到它的图像应该是不变的,因为在新的坐标系,它可以变换成 $Y=kX$ ,这样和原来的解析式一样,图像也一样
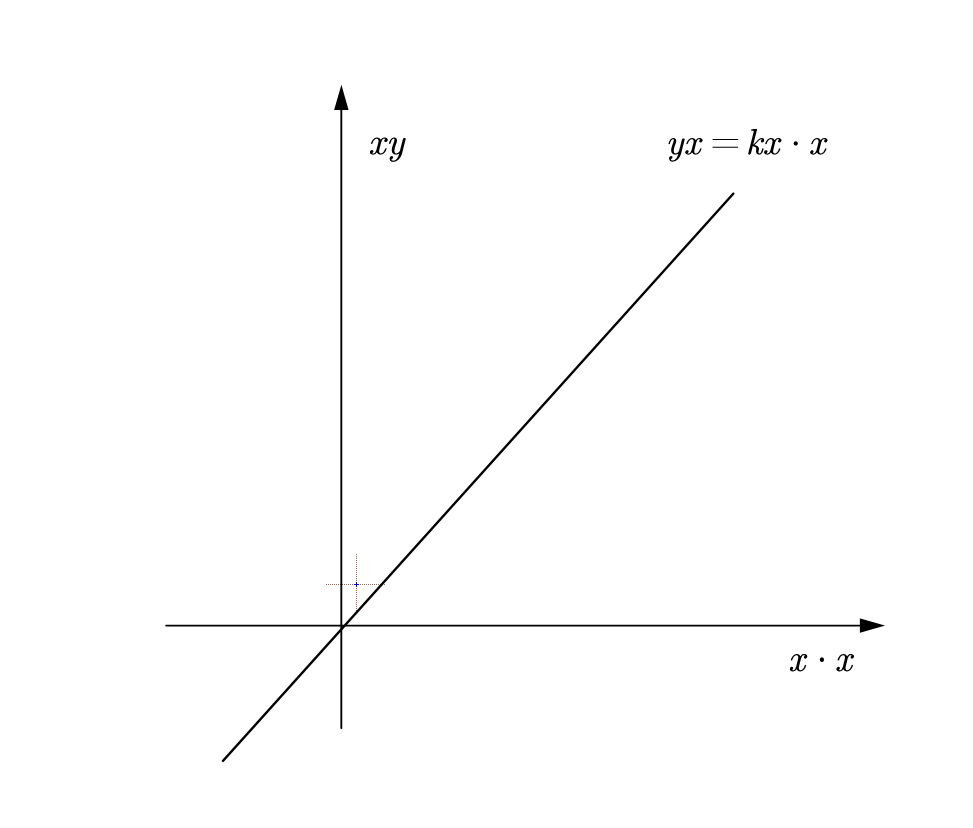
函数为一次函数
但是如果你用 $y=kx+b$,结果就不同了
如果这样,在新的坐标系里
$$Y=kX+b\sqrt{X}$$
得到图像如图所示(k取1,b取2)
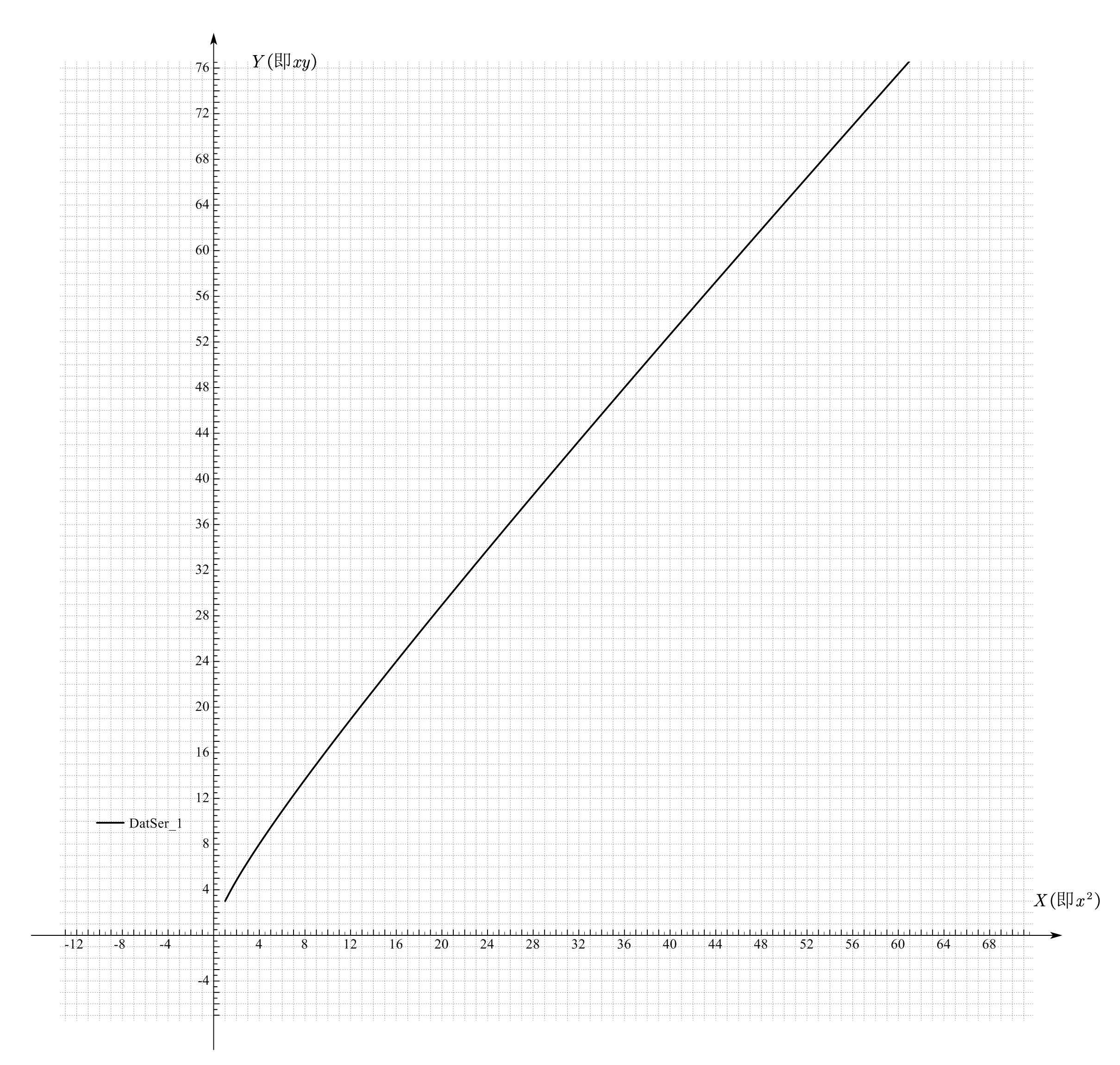
可以看到这不是一个直线(其实从X与Y的关系就能看出来)
直观地,变换后的函数会因为非线性因素被拉伸或扭曲.
规律的局部总结
那么是时候总结一下规律了
如果我们希望图像在新坐标系下,和原来的形状相同,就必须有:
$$Y=f(X)$$
而实际的 $Y$ 是:
$$Y=xf(x)$$
又有:
$$X=x^2$$
所以条件是:
$$f(x^2)=xf(x)$$
这个条件就是函数在这个非线性坐标系下“保持图像不变”的必要关系
这说明:
非线性坐标系会“选择性地”保留某些函数的形状.
这是一个非常深的结论
感觉怎么样?是不是还可以
其实这一步我真的想了很久,我想过很多种解释的方法,从原来非常长且难懂的部分不断精简才做到这样直观的表达
这或许就是我为什么写作的原因,因为分享不断提升表达
推广归纳梳理
前面是针对一种变换进行的规律探索,有了先前的尝试经验我们来推一下总的结论
变换形式推广
我们发现其实任何坐标系的变化,本质上都可以看作一个函数映射:
若将一个点在原坐标系中表示为:
$$(x,y)$$
则在一个广义坐标变换下,它可以被映射为:
$$(X,Y) = (\varphi(x,y), \psi(x,y))$$
其中:
$\varphi(x,y)$ 决定新的横轴含义
$\psi(x,y)$ 决定新的纵轴含义
一个坐标 = 一个输入 → 一个输出
是不是很像编码一样?
这说明了一个道理:
坐标系本质上是由一组函数定义的, 它并不刻画空间本身, 而是刻画我们“如何描述空间”.
当 $\varphi,\psi$ 为线性函数时,坐标系是线性的
当其为非线性函数时,坐标系便随之扭曲
因此:
所谓“非线性坐标系”,本质上就是一个非线性函数视角下的世界
条件推广
假设有一个原函数
$$y=f(x)$$
那么在原坐标系上选一个点:
$$P=(x,f(x))$$
经过坐标变换以后,它去了新地方:
$$P'=(X,Y)=(\varphi(x,f(x)),\psi(x,f(x)))$$
与此同时,在新坐标系里,有一条“新函数”:
$$Y=f(X)$$
我们从始至终的问题都可以理解为:
怎样才能让所有点仍然落在这条 新函数 上?
说直白点:
怎样让这两个点是同一个点?
那就必须满足:
$$Y=f(X)$$
代入变换结果我们可以立刻得到
$$\psi(x,f(x))=f(\varphi(x,f(x)))$$
我们之前推的那个
$$f(x^2)=x f(x)$$
其实只是这里的一个特例
当时我们选的是:
$$\varphi(x,y)=x^2,\quad \psi(x,y)=xy$$
带进去就是:
$$xf(x)=f(x^2)$$
完全一致
归纳梳理
对于变换中找不变性我们不能强行保持坐标不变
而是保持关系不变
重点不是变换前后点的位置
重点是这个点仍然服从同一个规则,即变换前后函数关系不变
如果一个世界被函数统治,那么不管怎么变坐标系,只要规则没变,世界就没变.
有点类似不变量理论,确实费了我很长时间
不忘初心
从目前的结论来看,由于我并不知道小灯泡的具体解析式,所以无法直接将结论机械套用到题目当中.但在这个过程中,我对“坐标系”“变量意义”和“规律保持的条件”有了更加清晰的认识,而这些认识本身,比得到选项答案更有价值.
也正因如此,我们在日常学习中应当始终保持一种“追问”的态度.不急于接受结论,而是反复思考它的成立条件与边界.
很多时候,结果只是一个终点,而思考的轨迹,才是真正扩展认知的过程.
结果固然重要,但真正改变人的,是走向结果的那条路.