今天老师给我了一道题,想了半天没想到怎么做辅助线,于是开始瞎尝试
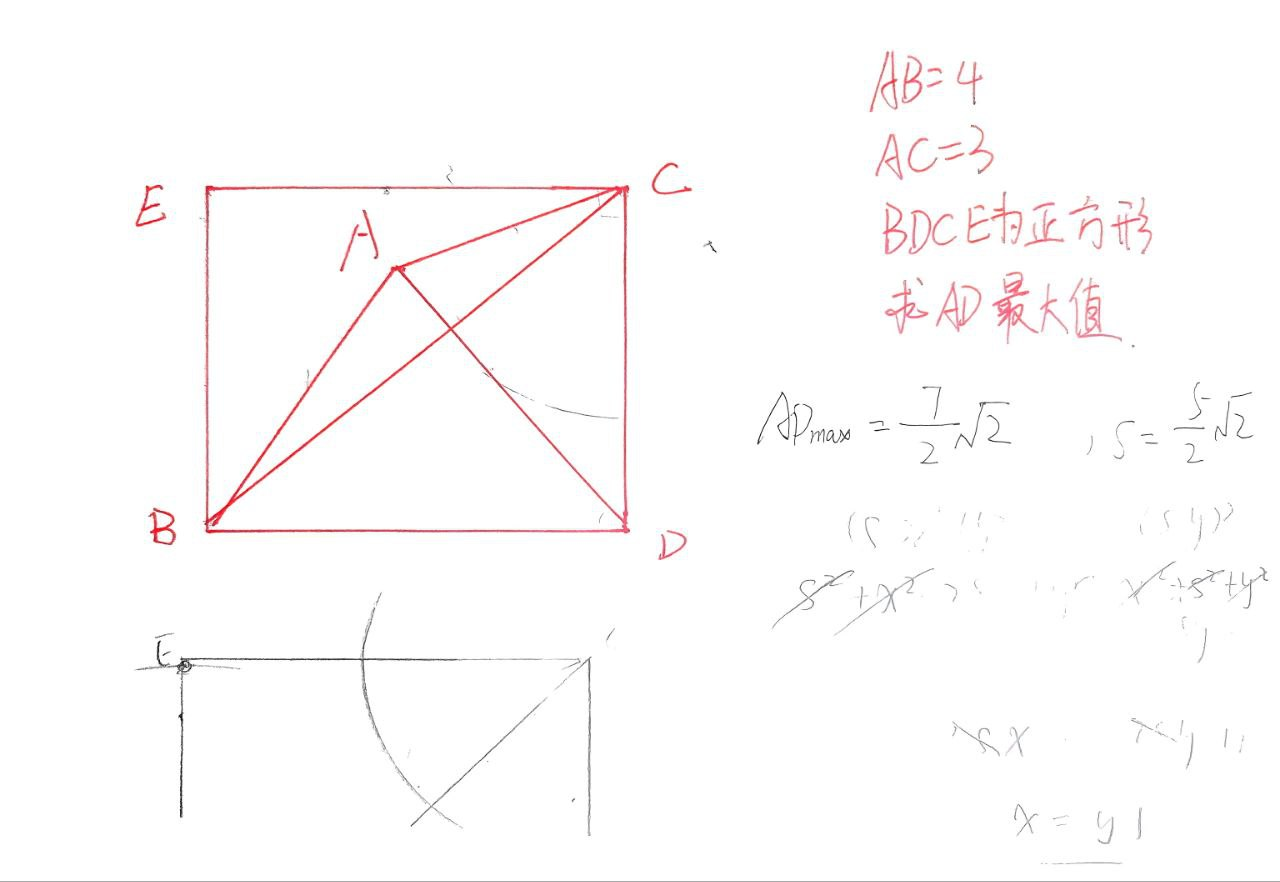
看上去十分眼熟但是发现实际上不太一样
于是想不出正解的我

关于这道题,我们可以抽象成两圆的交点与一点最大值的问题
这里参考图像相关
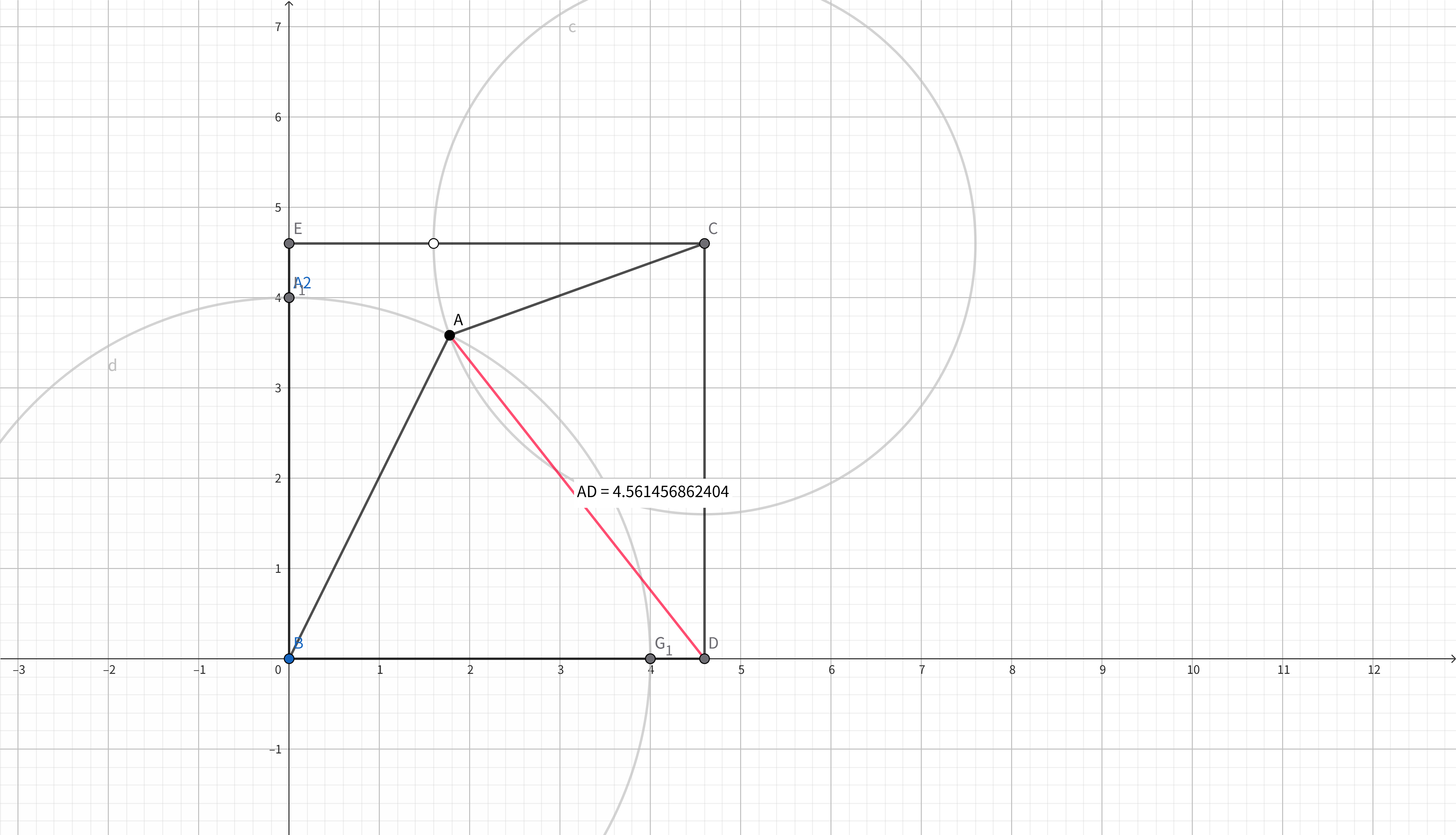
1.神奇的解法
设正方形边长为$s$
我们可以求得$B\left( 0,0 \right) ,E\left( 0,s \right) ,C\left( s,s \right) ,D\left( s,0 \right) $
作以$C$点为圆心,半径为$3$的$\odot c$,以$B$点为圆心,半径为$4$的$\odot d$
根据两圆交点坐标公式,有点$A$坐标:
$$A\Biggl( \;\frac{2s^2+7}{4s}\;-\;\frac{\sqrt{-4s^4+100s^2-49}}{4s}\;,\;\frac{2s^2+7}{4s}\;+\;\frac{\sqrt{-4s^4+100s^2-49}}{4s} \Biggr) \,\, \left( \text{注}:-4s^4+100s^2-49\ge 0,\text{两圆有交点} \right) $$
设$AD$距离为$D(s)$
欲求AD
令
$$m=\frac{2s^2+7}{4s}-\frac{\sqrt\Delta}{4s},\quad n=\frac{2s^2+7}{4s}+\frac{\sqrt\Delta}{4s},\quad \Delta=-4s^4+100s^2-49\;( \Delta\ge0)$$
则
$$m-s=\frac{7-2s^2-\sqrt\Delta}{4s},\qquad n=\frac{2s^2+7+\sqrt\Delta}{4s}$$
于是
$$(m-s)^2 =\frac{(7-2s^2)^2+\Delta-2(7-2s^2)\sqrt\Delta}{16s^2},\quad n^2 =\frac{(2s^2+7)^2+\Delta+2(2s^2+7)\sqrt\Delta}{16s^2}$$
相加得
$$(m-s)^2+n^2
=\frac{(2s^2+7)^2+(7-2s^2)^2+2\Delta+8s^2\sqrt\Delta}{16s^2}
=\frac{8s^2\bigl(25+\sqrt\Delta\bigr)}{16s^2}
=\frac{25+\sqrt\Delta}{2}$$
因此
$$D(s)={AD=\sqrt{(m-s)^2+n^2} =\sqrt{\frac{25+\sqrt{\Delta}}{2}}}=\sqrt{\frac{25+\sqrt{-4s^4+100s^2-49}}{2}}$$
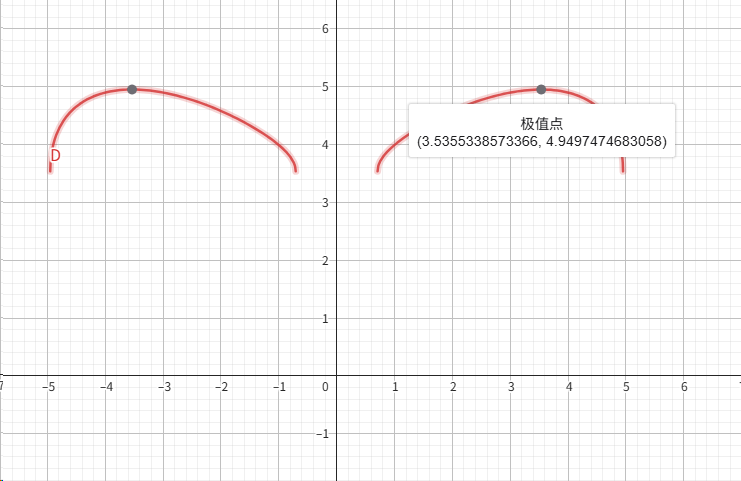
这是这个函数的图像(真像个笑脸)
我们知道, $AD$ 最大距离就是 $D(s)$ 的极值,接下来对极值进行求解
如果存在 $D\left( s_{\max} \right)$ ,即存在值 $s_{\max}$ 使 $D(s)$最大
那么 $D'(s_{\max})=0 $ 其中 $D'(s)$ 表示 $D(s)$ 的导数,这很好理解,到达最大值时坡度为$0$
也就是对$D(s)$进行求导,求 $D'(s)=0$ 时 $s$ 的值
为了计算便捷,我们令$F\left( s \right) =D\left( s \right) ^2$
可以注意到如果 $D(s_{\max})$ 的值为函数 $D(s)$ 的最大值,那么 $F(s_{\max})$ 也是函数 $F(s)$ 的最大值
且 $D'(s_{\max})=F'(s_{\max})=0$
$$\displaystyle F'(s)=\lim_{h\to0}\frac{F(s+h)-F(s)}{h}$$
令
$$F(s)=\frac{25+\sqrt{100s^2-4s^4-49}}{2},\quad
F_{2}(s)=100s^2-4s^4-49$$
那么
$$F\prime (s)=\lim_{h\rightarrow 0} \frac{F(s+h)-F(s)}{h}=\lim_{h\rightarrow 0} \,\frac{\frac{25+\sqrt{F_2(s+h)}}{2}-\frac{25+\sqrt{F_2(s)}}{2}}{h}
\\
=\lim_{h\rightarrow 0} \,\frac{1}{2}\frac{\sqrt{F_2(s+h)}-\sqrt{F_2(s)}}{h}$$
对分子有理化得到
$$\frac{\sqrt{F_{2}(s+h)}-\sqrt{F_{2}(s)}}{h}
=\frac{F_{2}(s+h)-F_{2}(s)}{h\bigl(\sqrt{F_{2}(s+h)}+\sqrt{F_{2}(s)}\bigr)}.$$
当 $h\to0$ 时,$\tfrac{F_{2}(s+h)-F_{2}(s)}{h}\to F_{2}'(s)$ 且 $\sqrt{F_{2}(s+h)}+\sqrt{F_{2}(s)}\to2\sqrt{F_{2}(s)}$,于是
$$F'(s)
=\frac12\;\frac{F_{2}'(s)}{2\sqrt{F_{2}(s)}}
=\frac{F_{2}'(s)}{4\sqrt{F_{2}(s)}}$$
再将 $F_{2}'(s)=200s-16s^3$ 代入,最终得到
$$F'(s) =\frac{200s-16s^3}{4\sqrt{100s^2-4s^4-49}}$$
求解 $F'(s)=0$ 得
$$F\prime (s)=\frac{200s-16s^3}{4\sqrt{100s^2-4s^4-49}}=0$$
去分母,得
$$200s-16s^3=0$$
提公因式,得
$$s\left( 200-16s^2 \right) =0$$
所以, $$s=0 或 200-16s^2=0$$
$s=0$不成立,排除
对于二次方程$-16s^2+200=0$
给定系数$a=-16,b=0,c=200$
则
$$s=\frac{-b\pm \sqrt{b^2-4ac}}{2a}=\frac{\pm \sqrt{-4\cdot \left( -16 \right) \cdot 200}}{-32}
\\
=\frac{\pm \sqrt{12800}}{-32}=\frac{\pm 80\sqrt{2}}{-32}
\\
s=\pm \frac{5\sqrt{2}}{2}$$
$s\geqslant 0,\text{取}s=\frac{5\sqrt{2}}{2}$
即 $s$ 取 $\frac{5\sqrt{2}}{2}$ 时,$AD=D(\frac{5\sqrt{2}}{2})$ 最大,代入得
$$D\left( \frac{5\sqrt{2}}{2} \right) =\sqrt{\frac{25+\sqrt{100s^2-4s^4-49}}{2}}
\\
=\sqrt{\frac{25+\sqrt{100\cdot \left( \frac{5\sqrt{2}}{2} \right) ^2-4\left( \frac{5\sqrt{2}}{2} \right) ^2-49}}{2}}
\\
=\sqrt{\frac{25+\sqrt{1250-625-49}}{2}}
\\
=\sqrt{\frac{25+24}{2}}=\sqrt{\frac{49}{2}}=\frac{7\sqrt{2}}{2}$$
即$D_{\max}=\frac{7\sqrt{2}}{2}$
$AD_{\max}=\frac{7\sqrt{2}}{2}$
2.正经解法
鸡爪模型构造手拉手
没看出来我是人机
