引入
在如今这个数字化的世界,我们不得不注册各式各样的在线账户。随着账户的增多,管理密码成为了一项艰巨的任务。为了简便起见,我们往往会为多个账户设置相同的密码,但这种做法显然存在安全隐患。与此同时,设置复杂且不同的密码又让人很难记住所有密码。这个时候,密码管理工具便成了我们的必备良伴。
在密码管理器这方面有很多APP,但是大多是收费的,你大概可以找到比较出名的1Password
确实这是一个非常好的密码管理器,他在安全,跨平台,UI都做的非常好,但是收费有点高
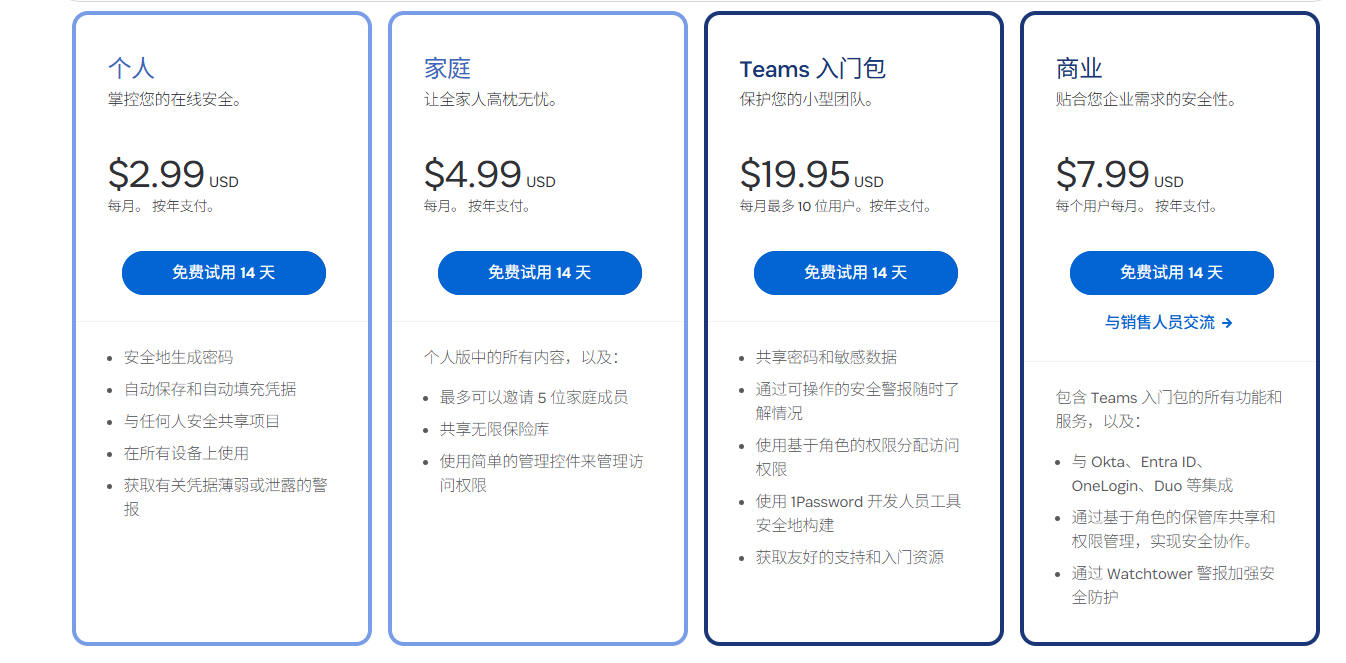
一个月二十多块就为了保存你的密码就有点不太值了
那么本文将会介绍一个免费的密码管理器:Enpass
介绍
其实虽说免费,但他其实不是免费的,它的桌面端是完全免费的,但是移动版需要付费(但其实有手段实现免费,后面会讲)
安全性
Enpass 的密码库默认存储在本地,用户的密码数据可以选择保存在本地设备上,不依赖任何云服务.这意味着你可以完全掌控数据,确保隐私性.当然你可以选择云服务,把密码文件托管到Google Drive、Dropbox、OneDrive 等,甚至可以自建云服务
Enpass的密码储存方式是通过主密码进行加密.你需要设置一个主密码并且确保永远不会忘记(如果你忘了等着重开吧),所有密码库数据在 Enpass 中都使用 256 位 AES 加密 来加密存储.即使数据存储在本地或云端,没有主密码的情况下,并且量子计算机没有问世,任何人都无法访问密码内容
主密码是用户访问 Enpass 密码库的唯一钥匙.Enpass 不会存储或记住主密码,因此只有用户自己才能解锁密码库.
下载/安装
通过下面链接可以在官网进行下载
基本使用
安装完应用会引导你创建账号和数据库,跟随引导进行就行
然后就可以使用了,非常简单
日常使用打开软件就需要主密码验证才能打开
密码页面可以自定义字段啥的比较好用
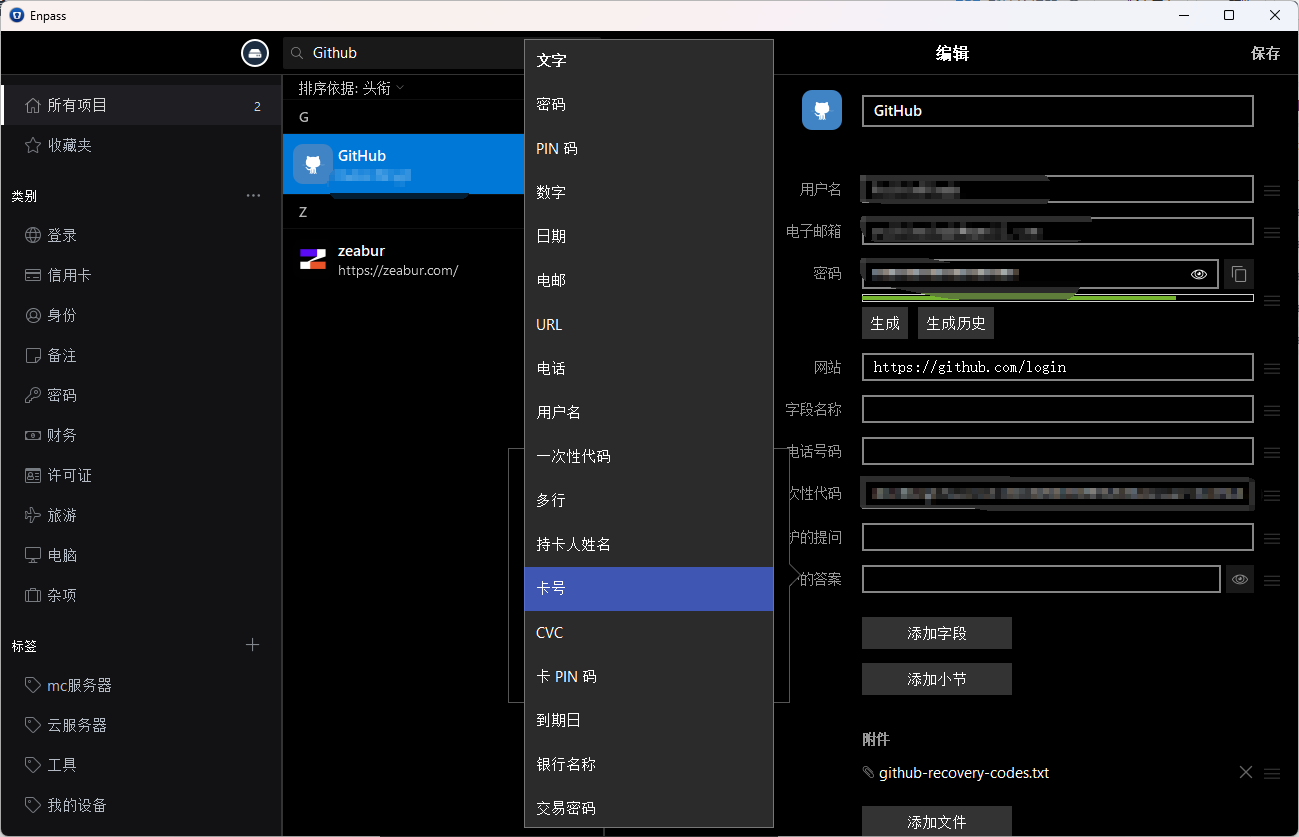
而且支持上传附件,我的Gtihub恢复文件就在上面
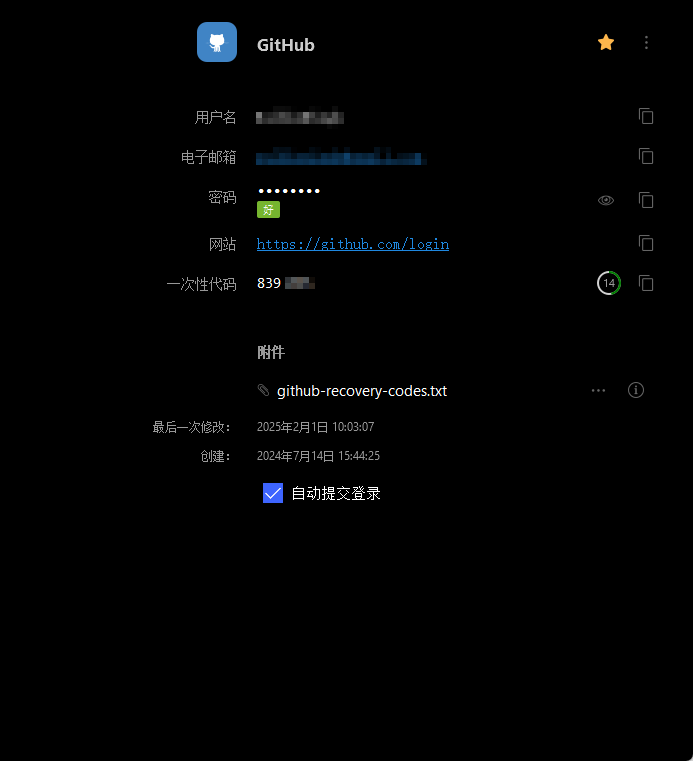
并且支持浏览器插件,可以自动填充
至于详细使用教程,我觉得是个人都能摸索出来
云服务
推荐使用坚果云存放你的Enpass文件
首先打开
然后在右上角点开账户信息
在安全选项添加应用Enpass(我已经添加了)
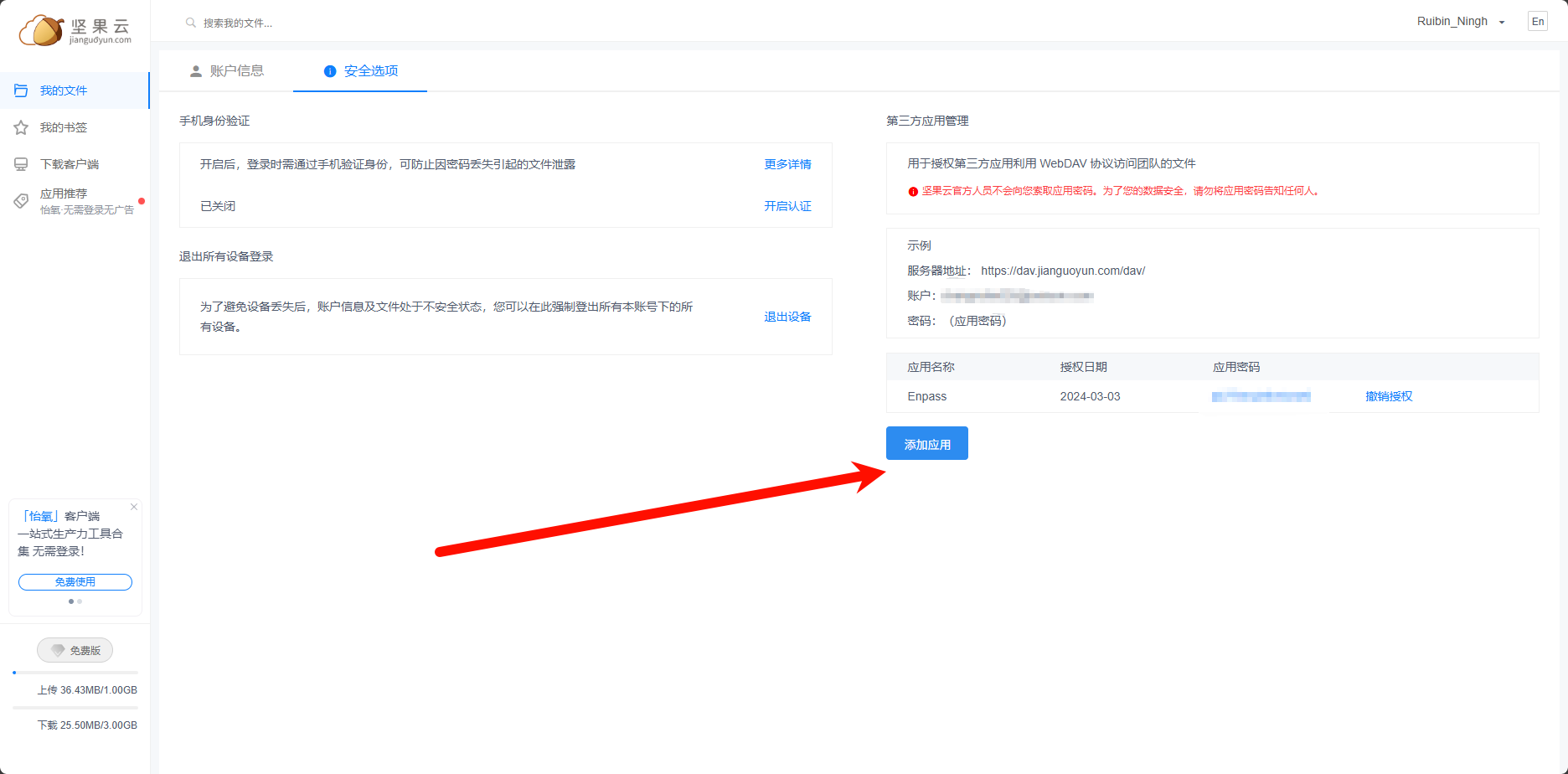
接下来打开Enpass
点击设置->保险库->主库->同步->设置同步
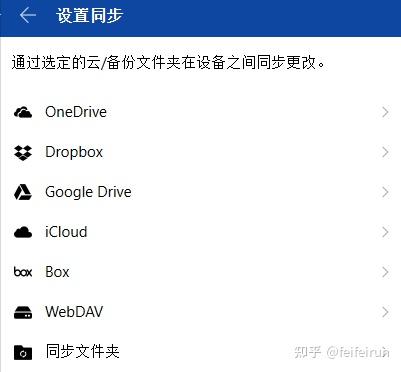
选择WebDAV,然后这样填
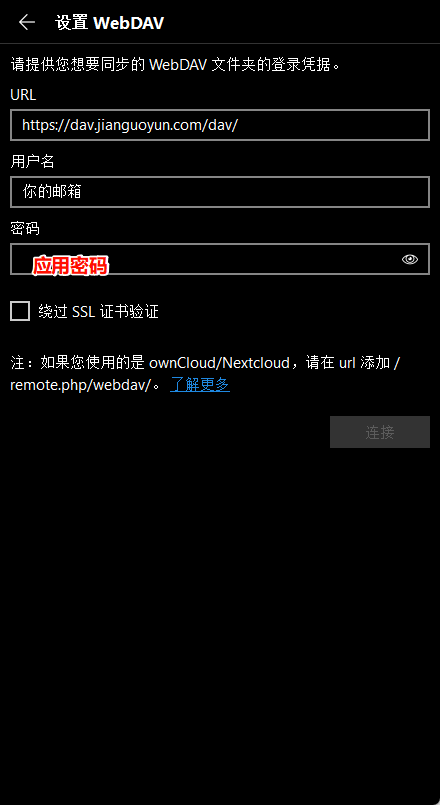
这样,就完成了云同步
当然你可以选择其他,甚至能自建一个服务,但是感觉有免费的就行了
至于安全性
你可能会问:要是这个云服务跑路了怎么办?
没关系,你的Enpass会自动同步一份备份在你的设备,就算云服务没了,还有最新的备份
移动版使用
花钱肯定是不可能的,那我们怎么在手机上用呢?
使用破解版
因为密码都在云,还有主密码加密,所以用破解版没啥危险(除非有恶意程序)
分享一下我的
Enpass6.11.14.1176-1759466392060.apk
至于IOS用户自求多福吧(