注:这是我第一次尝试在数学证明中分标题,实际上内容是连贯的,我觉得应该能更直观了解证明过程.关于证明过程我觉得代数证明有点烂,本人初中牲,写的不好勿喷
之前的题目让我想起推导两圆交点的坐标,于是这篇文章记录一下推导记录
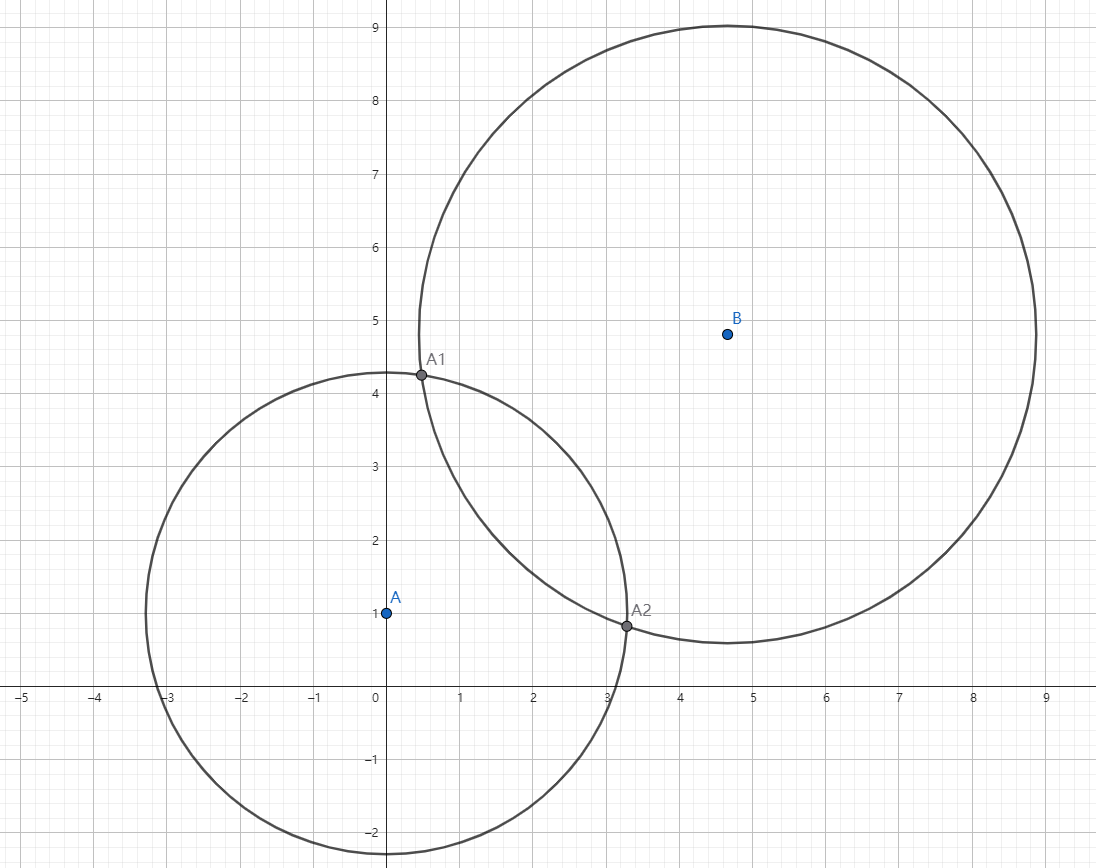
如图所示,现在有两圆 $\odot A,\odot B$ 相交与点 $A_1,A_2$ (如果只有一个交点可以看作 $A_1,A_2$ 重合)
我们的目的是求点的坐标
那么开始吧 :)
✦1.假设
我们令 $A\left( x_a,y_a \right) ,B\left( x_b,y_b \right) ,\text{两圆半径为}r_a,r_b,\text{交点坐标为}\left( x,y \right) $
连接 $AB$,令$$\varDelta x=x_b-x_a,\varDelta y=y_b-y_a$$ 如图所示
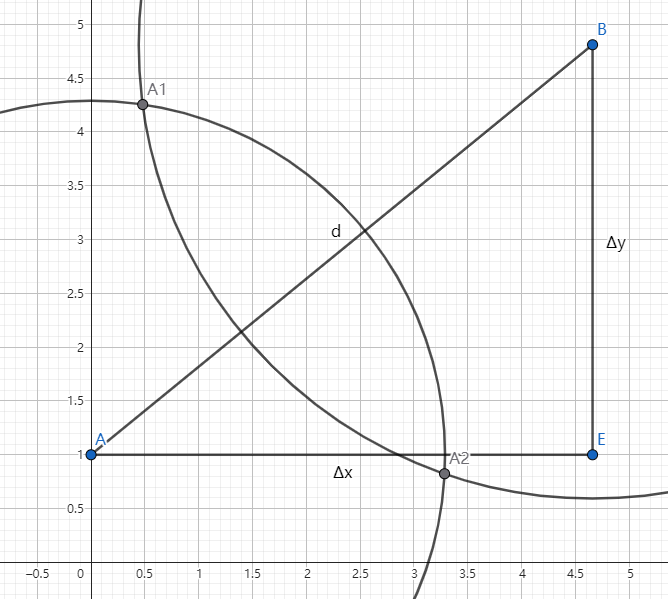
则圆心距$$d = \sqrt{(\Delta x)^2 + (\Delta y)^2}$$
✦2.判断交点情况
我们对交点情况进行讨论
$$\text{若}d>r_a+r_b,\text{则无交点}
\\
\text{若}d=r_a+r_b,\text{有唯一交点}
\\
\text{若}d<r_a+r_b,\text{有}2\text{个交点}$$
✦3.求解
✦3.1代数法
根据勾股定理或者是两点坐标距离公式,可以得到方程组
$$\begin{cases}
(x - x_a)^2 + (y - y_a)^2 = r_a^2\\
(x - x_b)^2 + (y - y_b)^2 = r_b^2
\end{cases}$$
 此时交点与方程组关系如图所示(相对于交点中的一点来说)
此时交点与方程组关系如图所示(相对于交点中的一点来说)
进一步展开,得
$$\begin{cases}
(x^2+x_{a}^{2}-2x_ax)+(y^2+y_{a}^{2}-2y_ay)=r_{a}^{2}\\
(x^2+x_{b}^{2}-2x_bx)+(y^2+y_{b}^{2}-2y_by)=r_{b}^{2}\\
\end{cases}
$$$$
\begin{cases}
x^2+y^2+x_{a}^{2}+y_{a}^{2}-2x_ax-2y_ay=r_{a}^{2}\\
x^2+y^2+x_{b}^{2}+y_{b}^{2}-2x_bx-2y_by=r_{b}^{2}\\
\end{cases}$$
也就是说如果交点存在,必须满足这两个方程
但是这是两个方程,我们要想办法凑成一个方程才好求
注意到两方程都存在 $x^2+y^2$ ,于是两方程做差,得
$$-2x_ax-2y_ay+x_{a}^{2}+y_{a}^{2}-r_{a}^{2}+2x_bx+2y_by-x_{b}^{2}-y_{b}^{2}+r_{b}^{2}=0$$
整理得
$$2(x_b-x_a)x+2(y_b-y_a)y=r_{b}^{2}-r_{a}^{2}+x_{b}^{2}-x_{a}^{2}+y_{b}^{2}-y_{a}^{2}$$
这是一个一次的方程(除了$x,y$其他都是常数项),同时交点也必须满足这个方程,我们成功地将这个方程组化为一个方程,而且可以认为这是一个一次函数
那么有一个问题,如果有两个交点,是不是都要满足这个函数,答案是肯定的
也就是说如果存在两个交点,他们都在这个函数的图像上,进一步的,这个函数的图像就是两个交点连线所在的直线
这是突破性的进展,我们引入之前定义的 $\Delta x,\Delta y$ ,移项去系数得到 $y$ 的表达式
$$y=\frac{r_{b}^{2}-r_{a}^{2}+x_{b}^{2}-x_{a}^{2}+y_{b}^{2}-y_{a}^{2}-2(x_b-x_a)x}{2(y_b-y_a)}
$$$$
=\frac{r_{b}^{2}-r_{a}^{2}+x_{b}^{2}-x_{a}^{2}+y_{b}^{2}-y_{a}^{2}-2\varDelta x\,\,x}{2\varDelta y}$$
我们只需要找到一个所有交点都会满足的方程代入即可求解,这里我选择前面的 $(x - x_a)^2 + (y - y_a)^2 = r_a^2$
代入后方程变为只含 $x$ 的方程,可以解出来 $x,y$
建议不要用代数法推导的通解公式(因为太长了甚至放不下),看到这一步就可以了,当然非想看可以看折叠的内容(写的不是很好凑合着看吧).
在实际运用代数法列出这个方程求解就行了(因为推导通解公式会涉及很多常量光展开都很费劲,实际计算的话这些都是明确的数),而且在数很庞大的时候不建议用代数法
代数法接下来的证明(点击左边三角展开)
这里有个问题,如果 $\Delta y=0$ 方程不成立(即两圆圆心在同一直线),所以针对$\Delta y$ 的取值进行讨论
✦3.1.1对 $\Delta y$ 的取值进行讨论
✦1.$\Delta y \ne 0$
根据前文对于 $y$ 表达式的推导
$$y=\frac{r_{b}^{2}-r_{a}^{2}+x_{b}^{2}-x_{a}^{2}+y_{b}^{2}-y_{a}^{2}-2\varDelta x\,\,x}{2\varDelta y}$$
防止公式太长超出显示范围,我们记
$$p = r_b^2 - r_a^2 + x_b^2 - x_a^2 + y_b^2 - y_a^2\\q = \dfrac{p}{2\Delta y} - y_a$$
则$$y = \frac{p - 2\Delta x \cdot x}{2\Delta y}= q - \frac{\Delta x}{\Delta y}x$$
代入方程$(x - x_a)^2 + (y - y_a)^2 = r_a^2$:$$(x-x_a)^2+\left( q-\frac{\Delta x}{\Delta y}x \right) ^2=r_{a}^{2}$$
展开得$$x^2+x_{a}^{2}-2x_ax+q^2+\frac{\Delta x^2}{\Delta y^2}x^2-2q\cdot \frac{\Delta x}{\Delta y}x=r_{a}^{2}$$
整理得$$\left( 1+\frac{\Delta x^2}{\Delta y^2} \right) x^2+\left( -2x_a-2q\cdot \frac{\Delta x}{\Delta y} \right) x+x_{a}^{2}+q^2-r_{a}^{2}=0$$
这是个二次方程,对于此方程,我们可以得知系数$$a=1+\frac{\Delta x^2}{\Delta y^2},b=-2x_a-2q\cdot \frac{\Delta x}{\Delta y},c=x_{a}^{2}+q^2-r_{a}^{2}$$
代入求根公式
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
最后整理得
$$\begin{aligned}
x_{1,2}&=\frac{2x_a+2q\,\tfrac{\Delta x}{\Delta y}\;\pm \;\sqrt{\bigl( 2x_a+2q\,\tfrac{\Delta x}{\Delta y} \bigr) ^2-4\bigl( 1+\tfrac{\Delta
x^2}{\Delta y^2} \bigr) (x_{a}^{2}+q^2-r_{a}^{2})}}{2\bigl( 1+\tfrac{\Delta x^2}{\Delta y^2} \bigr)},\\
y_{1,2}&=q-\frac{\Delta x}{\Delta y}\;x_{1,2}\\
\end{aligned}$$
✦2.$\Delta y = 0$
两圆方程为:
$$\begin{cases} (x - x_a)^2 + (y - y_a)^2 = r_a^2\\ (x - x_b)^2 + (y - y_b)^2 = r_b^2 \end{cases}$$
由于 $\Delta y = 0$,所以 $y_a = y_b$
两方程作差,得$$(x - x_a)^2 - (x - x_b)^2 = r_a^2 - r_b^2$$
可得表达式
$$x = \frac{r_a^2 - r_b^2 + x_b^2 - x_a^2}{2\Delta x}$$
记:
$$k = \frac{r_a^2 - r_b^2 + x_b^2 - x_a^2}{2\Delta x}$$
然后代入圆A方程:
$$(x - x_a)^2 + (y - y_a)^2 = r_a^2$$ $$(k - x_a)^2 + (y - y_a)^2 = r_a^2
\Rightarrow
(y - y_a)^2 = r_a^2 - (k - x_a)^2$$
设右侧为 $H$,即:
$$H = r_a^2 - (k - x_a)^2$$
若 $H < 0$,无实数解,两圆不相交
若 $H = 0$,交点唯一
若 $H > 0$,有两个交点
$$y = y_a \pm \sqrt{H}$$
因此两交点为:
$$(x_1, y_1) = (k, y_a + \sqrt{H}),\quad
(x_2, y_2) = (k, y_a - \sqrt{H})$$
✦3.特殊情况
若$\Delta x = 0,\Delta y = 0$
-若 $r_a = r_b$,两个圆重合,交点有无穷多个
-若 $r_a \ne r_b$恒无交点
✦3.2几何法
我们已经领略到了代数法的臃肿,传统建系直接求会造成庞大的计算量,所以我们另辟蹊径,从几何的角度分析
未完待续...
📒日志
2025年7月12日12:50:55 完成代数法的证明
2025年7月30日18:57:37 最近事情有点多,在8月3日前完成证明