我是一名物理爱好者,总喜欢追问现象背后的本质。面对教科书里那些只给结论、不解释原因的内容,我总忍不住反思:这些知识能不能从更底层的角度理解?
于是,我尝试重新整理电学的基本理论,希望用更直观、更本质的方式解释其中的规律,而不仅仅是照搬定义和公式。
本篇文章面向已经具备一定电学基础的初学者。如果你对电路有基本了解,可能会从中发现一些与教科书不同的视角。
我要声明的是:
我不会像教科书那样重复已有内容。
如果你只是想刷题、提分,这篇文章可能显得理论性过强。
但如果你像我一样,想理解为什么电流会流、电压为何存在,这篇文章会为你提供一个不同的思路,也许能激发你对物理的兴趣。
基础
在进入电学世界之前,你必须对分子、原子、电子有最基本的认识。因为接下来的一切,都是建立在它们之上的。
此外,你需要稍微了解一些初中电学,因为我不可能讲太多
电是什么
既然要学电学,那么我问你,电是什么?
电其实是一种物理现象,我们先了解现象在究其本质
那么我们从人类认识电开始讲起,这就要回到古代了
人类最早认识到电,根本不是因为会发电,而是因为这几件怪事:
琥珀摩擦后能吸小纸屑
闪电能把树劈成两半
两根金属棒靠近会「互相吸 / 互相推」
电通过导线能让灯泡发光、让电机转动
被静电电过会“麻”和“疼”
这些现象看起来五花八门,但它们有个共同点:
某种看不见的东西,在远距离、无接触的情况下,还能施加“力”和“能量”
于是问题来了:
是什么东西在“隔空使劲”?
经过不断的研究
人们发现了一些规律:
不是所有物体都能这样
只有一些物体才具有这些性质,为了方便称呼我们称发生这种现象的物体"带电"
而且还有两种完全相反的表现:
有的靠近会吸引
有的靠近会排斥
规律出现了:
存在两种不同的“电性”,并且
相同的互相排斥,不同的互相吸引
人类给它们起名:
正电(+)
负电(-)
但这还只是现象分类,不是本质。
但是你不需要了解太多,这就是电,没错,电是一种物理现象,并没有那么复杂
如果不信这是更严谨的定义:
电是带电荷的物体与电场之间的相互作用以及电场性质相关的物理现象
电荷
人们最早注意到一些奇怪的现象:
摩擦过的琥珀可以吸起轻小的物体(如纸屑、羽毛); 带有相同电性的物体靠近会相互排斥,带有不同电性的物体靠近会相互吸引; 电流可以让灯泡发光、电机转动。
于是,人们把这种现象称为:物体带电,也就是说物体“带有电荷”。
进一步观察发现,这些现象背后似乎隐藏着几个重要规律:
物体具有一种“吸引或排斥其他物体”的能力;
这种“吸引/排斥”的能力是可以累积的,有强有弱;
当两个带相反电性的物体相互接触时,它们的带电程度会减弱,甚至可能消失。
这时,人们开始思考一个问题:
我们能不能给这种“吸引和排斥的能力”一个统一、可量化的物理概念?
于是,科学家引入了“电荷量”q,用来描述物体带电的多少。
但仅仅有“电荷量”这个概念还不够,它还需要一个单位。实验进一步表明:
电荷不会凭空产生,也不会凭空消失,只能从一个物体转移到另一个物体; 不同物体的电荷量可以直接进行加减; 因此,电荷可以像长度、质量一样,被当作一个可以测量、可以运算的物理量。
既然物体是由原子构成的,那么,电荷量的最基本单位是否也可以从原子中找到呢?
通过研究人们发现:原子由原子核和电子组成,而原子核中又包含质子和中子。进一步研究发现:
质子和电子都带电,并且在一个正常原子中,质子的数量与电子的数量恰好相等,而原子整体却不显电性,
这说明:质子与电子所带的电荷量大小相等、符号相反。
于是,人们将这种最小的电荷量作为标准,称为基元电荷(或元电荷),用符号 e 表示:
$$1e = 1.602\,176\,634 \times 10^{-19}\, \text{C}$$
它在数值上等于一个电子所带电荷的大小,也等于一个质子所带电荷的大小。
并且,任何物体的总电荷量,总可以表示为基元电荷的整数倍:
$$q = n \cdot e$$
其中:
$q$ 物体的总电荷量(单位:C,库仑)
$n$ 所带电荷的数量(整数)
$e$ 基元电荷 $1.602\times 10^{-19}\text{C}$
换句话说,人类并不是先“发明”了电荷量这个概念,而是被自然界中无数次的吸引与排斥现象,一步步“逼”出了这个概念。
值得一提的是,我们通常约定单位正电荷作为参考,于是电荷量可以取正,也可以取负。
具体来说:
正电荷的电荷量取正值,负电荷的电荷量取负值,这样做的目的,是为了区分电荷的种类,而不是单纯地在“数数”。
试想一下:
一个物体内部可能有天文数字般多的正电荷和负电荷,但如果它们数量相等、位置分布均匀,那么这个物体对外几乎没有任何电的表现——它是电中性的。
如果此时我们仍然把内部所有电荷都算进“电荷量”,
那一个普通的、看起来再正常不过的物体,电荷量可能是个极其夸张的数字。
这既不符合直觉,也不利于计算。
因此,物理上更关心的是:
这个物体“对外表现出”的那部分电荷
也就是正负电荷相互抵消后剩下的“净电荷量”。
这才是真正有意义、能参与电场、电势、电流等现象的电荷量。
电场
说完了电荷,我们来思考这个问题
你先看几个现象:
琥珀摩擦后能吸纸屑
带电物体靠近轻小物体会让它移动
闪电劈下来
注意,这些现象有一个共同点:
电荷并不直接接触物体,它隔空产生作用。
所以必须有一个“东西”在电荷和被作用物体之间传递力。这个“东西”就是电场的起点。
我们通过实验实验总结:
任何电荷都会影响它周围的空间
力的大小与电荷量、距离相关(库仑定律)
多个电荷的影响可以叠加(叠加原理)
于是科学家抽象出一个概念:
电场:描述空间中每一点受到单位正电荷作用力的向量场
也就是说,电场不是物质,而是一种空间性质。它告诉你:
在某点放一个小正电荷,它会受到多大力
力的方向向哪里
是不是有点晕,没事,初中范围内不考这些,你只需要知道电场对电荷有作用力就好了
初中范围内根本无法进行电场相关计算,所以先省略了
电势和电压
想象几个常见的情况:
你把摩擦后的塑料棒靠近小纸屑,小纸屑被吸起来
带电的金属球让别的金属球运动
电池两端插灯泡,灯亮
因为同种电荷相互吸引,异种电荷相互排斥
你会发现:
电荷有移动的趋势
并且这种趋势不是随便动,而是“从某个地方往另一个地方”
这就是我们引入电势的原因。
电势
我们已经知道:电荷之间存在作用力。
正因为存在这种力,当一个电荷处在电场中不同位置时,它所具有的能量也会不同,这种与电场位置有关的能量,叫做电势能。
也就是说:
电势能,是“电荷”由于所处位置不同,而具有的能量。
那么问题来了:
如果在某一点放一个大电荷,它的电势能大;
放一个小电荷,它的电势能小。
这说明:电势能不仅和位置有关,还和电荷量有关。
为了只研究“这个位置本身的能量特征”,而不受电荷大小的影响,人们把电势能“平均到每单位电荷上”,引入了一个新的物理量——电势。
再看看它的定义:
$$V = \frac{U}{q}$$
$V$ 电势,单位:伏特(V),也就是焦耳每库伦(J/C)
$U$ 电势能,单位:焦耳(J)
$q$ 电荷量,单位:库仑(C)
表示某点的电势 = 单位正电荷在该点具有的电势能
公式带单位就变成:
$$\text{V (伏特)} = \frac{\text{J (焦耳)}}{\text{C (库仑)}}$$
我们之前讲电荷量是有正负的,那么如果引入这条电势就是每单位正电荷的电势能,此时负电荷的电势和电势能也是负的
值得注意的是电势,是位置的属性;电势能,是电荷的属性。
电压
了解了电势之后,我们就可以自然地引出“电压”。
先做一个思想实验:
想象你是一个电子,处在一个电场当中。 你的周围并不是一片“均匀的空间”,而是有的地方电势高,有的地方电势低。
这里要先澄清一个非常重要的点:
电势的高低,并不等价于“正电荷多 or 负电荷多”, 而是代表:在这个位置上,单位正电荷所具有的电势能高还是低。
对你(一个负电荷)来说:
当你来到电势高的地方,你的电势能会 减小(因为 $U = qV$,而你的 $q < 0$ )
当你来到电势低的地方,你的电势能会 增大
而自然界有一个“偷懒定律”—— 一切事物都倾向于向势能更低的状态发展。(能量最低原理)
所以,电子会自发地朝着“电势更高的地方”运动,是为了让自己的电势能降低。
而正好相反,正电荷则会自发地朝着“电势更低的地方”运动。
于是原来的结论,可以更严谨地写成:
正电荷 → 电势低的地方
负电荷 → 电势高的地方
但注意: 真正推动它们的,不是电势本身,而是“电势的差异”——也就是变化。
如果整个空间的电势都一样,高也好低也好,电荷根本“没有理由移动”。
这就像一片完全水平的地面,没有高低差,你根本不会滚动。
而一旦出现高低差——坡度就出现了。
这个“坡度”,在电学中,叫做:电压,也叫电势差。
如果在 A 点和 B 点之间存在电势差,那么:
$$U_{AB} = V_A - V_B$$
这个 $U_{AB}$,就是从 $A$ 到 $B$ 的电压,单位仍然是伏特($V$)
你可以这样理解它的本质:
电压 = 电势在空间中的“落差” 就像高度差,会让水流动;电势差,会让电荷运动。
但要特别强调的是:
电压不是力
它只是一种“条件”或者“推动趋势” 真正产生力的,是电场
电压更像是:“这个地方有多陡”。
电流
我们知道,有电压就意味着存在电势差。
而一旦存在电势差,空间中就会形成电场。
根据电荷的基本性质
同种电荷相互排斥,异种电荷相互吸引。
在电场中:
正电荷会趋向于电势较低的地方运动, 负电荷则会趋向于电势较高的地方运动。
这是因为它们在运动过程中,电势能会不断降低,而自然界的系统总是趋向于更稳定、能量更低的状态。
既然电荷在电场中会受到力的作用,那它们就不再是“无序乱动”,而是开始有方向地移动。
这种电荷的定向移动,我们称之为——电流。
电流方向,按规定取为正电荷移动的方向。 但在金属导体中,真正移动的并不是正电荷(质子几乎固定在原子核中),而是带负电的电子。 因此,在实际电路中,电子的运动方向与电流方向相反。
之所以会这样定义,是由于早期人们尚未发现电子的存在,这个规定保留至今,成为了一种“历史遗产”。
那么,电流是如何形成的呢?
根本原因只有一个:存在电压(电势差)。
正是由于两点之间的电势不同,才使电子在电场力的作用下发生定向移动,从而形成持续的电流。
这也是为什么,我们必须先理解电势,再理解电压,最终才能真正看懂电流的本质。
在物理上,电流被定义为: 单位时间内通过导体横截面的电荷量。
其数学表达式为:
I = \frac{\Delta Q}{\Delta t}
其中:
\Delta Q:在时间 \Delta t 内通过的电荷量,单位是库仑(C)
\Delta t:时间间隔,单位是秒(s)
I:电流,单位是安培(A)
由此可知:
1 \text{A} = 1 \text{C} / 1 \text{s}
电流的本质,其实就是电荷流动的快慢程度。
电阻
电荷在导体中的运动并不是一帆风顺的。
在微观尺度上,电子在运动过程中会不断与原子、离子以及晶格结构发生碰撞,使它们的运动受到阻碍。
这种“阻碍电荷做定向运动的能力”,就称为电阻。
对一段导体来说,加在它两端的电压 $U$ 与通过它的电流 $I$ 之比,称为这段导体的电阻,记为 $R$:
$$R=UIR=\frac{U}{I}R=IU$$
这个式子说明:在相同的电压作用下,如果通过导体的电流越小,就说明它对电荷定向运动的阻碍越强,也就是它的电阻越大。
如果导体中完全没有电阻,那么电子在电场力的作用下就会持续加速,速度会越来越大。但在现实中,电子不断与原子发生碰撞,能量被消耗,这使得它们的速度只能维持在一个稳定值附近,而不会无限增大。
因此,正是由于电阻的存在,电流才不会失控增长,而是保持在一定范围内。
需要注意的是
电阻的“定义”是人为规定的,为了量化阻碍能力,而不是物理定律。
这个会在欧姆定律讲到
欧姆定律
前面说了我们通过推理得出电阻与电流电压的基本规律,但是这不是最终结果,我们仍无法说明当电阻一定时,电流与电压是线性关系
直接去理论证明太难了,还是通过做实验得到规律比较简单
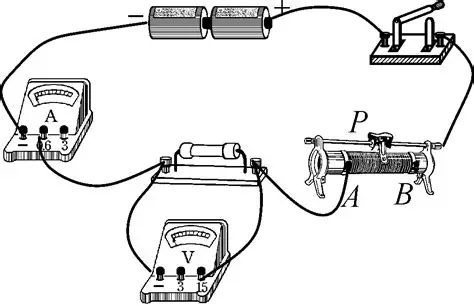
如图,我们通过这样的实验来探究一个导体电流,电压,电阻三者的关系
那么如何探究?
很简单,你想要探究哪两个量之间的关系只需要让第三个量不变就好了
如果我不改变定值电阻的电阻,那么通过记录电流表与电压表示数,再通过滑动变阻器调节电压获得更多参数,我就可以获得结论了
这里需要注意,滑动变阻器可以改变自身的电阻,当滑动变阻器电阻变大,整个电路的电阻也应该变大,那么根据之前的推理,总电压是恒定的,电流应该变小,进而我们可以获得不同的数据.
这里不多说了,都很基础
总而言之通过实验得到了一个结论:
对于一定温度下的部分导体,电流 $I$ 与两端电压 $U$ 成正比,与导体电阻 $R $ 成反比
$$I = \frac{U}{R}$$
这正好和电阻的规定相同
但是需要注意是
1.仅限部分导体,因为大多数情况下导体的电流与电压不成线性关系,这种导体叫非线性元件
大部分金属导体在常温下变化呈线性关系
2.这不是“自然法则”,而是实验总结出来的规律,适用于大部分金属导体、常温、低电压的情况。
3.在高温、半导体或非线性元件中,电流和电压不再严格成比例,欧姆定律只是近似成立。
4.微观上,欧姆定律反映的是电压提供推动力,电子在导体内受阻碍(碰撞)后维持稳定漂移速度。
总结一下
欧姆定律适用于温度恒定、纯电阻元件、低电压低电流的线性条件下,是电压与电流成正比的经验规律
它的使用范围很局限,如果条件不满足就无法使用
关于纯电阻是什么,我们在电功讲
电路
这部分是教科书主要讲的部分
没有什么意思,所以我简单略过没用的
至于一些有意思的我会讲一些
串联电路分压特点
课本上会通过实验的方式证明串联电路的电流相等,电压按电阻分配
但是为什么?
串联电路中,所有元件共用同一条电流路径
理论上,电荷在导线里是连续的,同一时间流过每个元件的电荷数相同,否则电荷会在节点处堆积,形成不稳定状态。
电流又是单位时间内通过导体横截面的电荷量
自然各个点的电流相等
至于电阻按电压分配
由于电流 $I$ 相同,但各个元件的电阻不同。
电压 $U = IR$,所以阻值大的元件两端电压高,阻值小的元件两端电压低。
可以这样理解:电阻越大,需要的电场力越大才能让相同电流通过
并联电路的分流特点
首先电压相等
并联的每条支路都直接连接在同两点上
电势差(电压)相同,这是因为电势差是两个节点间的属性,每条支路端点对应的节点电势一样
电荷在各条支路上看到的“坡度”是一样的,所以电压一样
其次电流按电阻分配
根据欧姆定律 $I = \frac{U}{R}$
电压一样,电阻小的支路电流大,电阻大的支路电流小。
阻碍小的地方,电子更容易流过去;阻碍大,电子“流不动”,于是分流不均
电功
电功很简单明了了,就是电流做功的大小
那么之前讲了电子的运动基于电势差,所以平均一个电子做的功就是 $U\cdot 1\mathrm{J}$
推广一下,假设电荷量为 $q$ ,则电功为
$$W=qU$$
又因为电流的定义是单位时间内通过的电荷量,即
$$q=It$$
所以
$$W=UIt$$
总结
本文并不是为了替代教科书,而是试图回答教科书常常回避的问题:
这些公式与定义,究竟从哪里来?它们描述的真实物理图景是什么?
通过从电荷、电场、电势、电压一直追溯到电流与电路规律,我们可以看到:
电不是“电流在流”,而是带电粒子在电场作用下的定向运动
电压不是“推动力”,而是空间中电势的差异
电流不是原因,而是电势差存在后的结果
欧姆定律不是自然公理,而是在特定条件下成立的经验规律
这些结论在考试中未必直接出现,但它们决定了你是否真正“理解”了电学,而不只是会代公式。
如果你只是希望快速提分,那么熟记公式已经足够;
但如果你希望在以后学习高中物理、乃至更深入的电磁学时少走弯路,那么从现象 → 本质 → 抽象模型的角度去重新理解这些概念,是非常值得的。
物理并不神秘。
它只是把世界中反复出现的现象,用尽可能简洁、统一的方式描述出来而已。